Recursion

Overview

We can define the factorial of a number as follows:

$x! = x \times (x - 1) \times (x -2) ... \times 2 \times 1$

If we want to write a Java function that computes the factorial of a number, we can do it with a loop like so:


public static int fact(int x) {
    int product = 1;
    while (x > 1) {
        product = product * x;
        x--;
    }

    return product;
}

Alternatively we could define the factorial of a number recursively like so:

$x! = x \times (x - 1)!$

This means that the factorial of a number x is equal to x times the factorial of x - 1. If we use this definition for 5!, we would have:

$5!= 5 \times 4!$

Then replacing 4!, we get:

$5! = 5 \times 4 \times 3!$

If we keep going, we'll get:

$5! = 5 \times 4 \times 3 \times 2!$

Next, we have:

$5! = 5 \times 4 \times 3 \times 2 \times 1!$

If we keep expanding like this, however, we will never be able to stop:

$5! = 5 \times 4 \times 3 \times 2 \times 1 \times 0 \times -1 \times -2 ...$

Which will give us zero.

When using a recursive definition like this, we will have to specify when to stop. In the factorial definition, we can say that the factorial of 0 is 1, and otherwise it's the recursive definition:

$0! = 1$

$x! = x \times (x - 1)!$

Now when we expand a factorial, we will stop at x = 0, and just use the value 1 instead of expanding on forever. Mathematicians frequently use recursive definitions like this.

We can use recursive definitions like this to write code as well. To do this, we just have a function that calls itself. Following is a factorial function based on the recursive definition:


public static int fact(int x) {
    if(x == 0) {
        return 1;
    } else {
        return x * fact(x - 1);
    }
}

How Recursion Works

If we call fact(4), then we will start to execute the fact function with 4 as a parameter. In doing so, we call fact(3) which then begins to execute. Then fact(2) gets called which calls fact(1) which calls fact(0).

fact(0) stops the recursion by just returning a value of 1 directly. Then the program goes back to where it left off in fact(1) and multiples 1 * 1 and returns 1. Then we are back where we left off in fact(2) which multiplies 2 by the result of fact(1) or 1 giving 2.

fact(2) then returns that 2 up to fact(3) which multiplies 3 by the 2 to get 6. The 6 is then returned up to fact(4) which multiplies 4 by the result of fact(3) or 6 giving 24. Then fact(4) returns to where it was called at with the final answer of 24.

Infinite Recursion

If the factorial function forgets to check for the 0 value, and always calls itself like so:


public static int fact(int x) {
    return x * fact(x - 1)
}

Then we run into something called infinite recursion. Infinite recursion is like an infinite loop, except that it will eventually crash the program.

Whenever a function is called, the computer needs to store information for that function (on "the stack"). The stack is only so big, so if we keep calling a function over and over, without returning, the stack will overflow.

Whenever writing a recursive program, it's important to make sure that there is always a "base case" that returns something directly. The recursive case should then move us closer to the base case so that the recursion will eventually stop.

Example: Printing Digits

Say we wanted to print an integer with one digit on each line, backwards. So 12345 would be printed as:

How could we do that with recursion?


import java.util.Scanner;

class Vertical {

    // write a number vertically
    public static void writeVertical(int num) {

        
    }

    public static void main(String args[]) {
        int number;
        System.out.print("Enter a number: ");
        Scanner in = new Scanner(System.in);
        number = in.nextInt();
        writeVertical(number);
    }
}

Now what if we wanted to print the digits in forwards order so the output would be:

What change would we have to make to our code above?

Recursion is very good for doing things in reverse!

Finding the Sum of a Range of Numbers

How could we use recursion to find the sum of a range of numbers?


import java.util.Scanner;

class Range {

    private static int moves = 0;

    public static int sumRange(int start, int end) {


    }

    public static void main(String args[]) {
        System.out.print("Enter the start and end: ");
        Scanner in = new Scanner(System.in);
        int a = in.nextInt();
        int b = in.nextInt();
        System.out.printf("Sum from %d to %d is %d.\n", a, b, sumRange(a, b));
    }
}

Towers of Hanoi

There is a myth that there is a temple with three large towers. On the first tower are 64 golden rings where each one is smaller than the one under it. Monks at the temple are trying to move all of the rings from the first tower to the third tower.

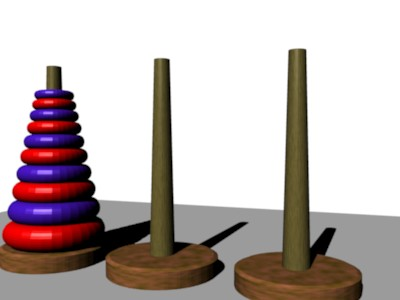
However they must obey the rule that no ring can be placed on a ring that is smaller than it. To move the rings, they must use the third tower as a place holder to move the rings over while obeying the rule.

The myth states that when the monks are finished, and have moved all 64 rings to the third tower, the world will end.

We want to write a program that will figure out how to move all of the rings over, one by one.

Thinking of this recursively, to move any disc from the left tower to the right tower, we would first have to move all of the discs above it to the middle, then put the disc we want on the right, and then put all of the discs on the middle tower back on top at the right.

This is recursive because in defining how to move a disc, we say that we have to move other discs. This idea can be used to come up with a recursive algorithm like so:


To move a disc from left to right, using middle:
    First move all discs above us to the middle, using right.
    Then move this disc from the left to the right.
    Lastly move all discs from the middle to the right using left.

This program demonstrates this algorithm:.


import java.util.Scanner;

class Towers {
    private static int moves = 0;

    public static void moveDisc(int num, int from_tower, int to_tower, int temp_tower) {
        if (num > 0) {
            moveDisc(num - 1, from_tower, temp_tower, to_tower);
            System.out.printf("Move a disc from tower %d to %d.\n", from_tower, to_tower);
            moves++;
            moveDisc(num - 1, temp_tower, to_tower, from_tower);
        }
    }

    public static void main(String args[]) {
        System.out.print("Enter the number of discs: ");
        Scanner in = new Scanner(System.in);
        int number = in.nextInt();

        // move this many discs from tower 1 to tower 3, using tower 2 as a temporary spot.
        moveDisc(number, 1, 3, 2);
        System.out.printf("%d moves were made!\n", moves);
    }
}

This function calls itself twice each time through. This means the total number of steps needed doubles for each additional ring that we add. The number of moves is given in the following table:

Rings	Steps
1	1
2	3
3	7
4	15
5	31
6	63
7	127
8	255
9	511
10	1023
...	...
64	18446744073709551615

The number of steps is defined by the following formula:

$steps(rings) = 2^{rings} - 1$

For doing a small number of discs, this doesn't take too terribly long. On my computer, given how long smaller numbers of discs take, it will take roughly 17 million years for the program to complete if we try all 64. Given that the monks are probably a lot slower than a computer, the world won't be ending any time soon :).

Designing Recursive Functions

Break big problems into smaller ones.
Make sure there is a base case.
Make sure the general case gets us closer to the base case.