Merge Sort

Overview

As a last example of recursion, we will look at the merge sort algorithm. We have already seen the bubble sort algorithm for sorting which uses loops. Bubble sort is not very efficient, but is easy to write.

Merge Sort Algorithm

The merge sort algorithm is fundamentally very simple:

To merge sort an array:
1. If the array has 0 or 1 items, then stop as it is already sorted.
2. Merge sort the left half of the array.
3. Merge sort the right half of the array.
4. Merge the two sorted halves together to make a new, sorted, array.

The following image depicts how the merge sort algorithm would sort an array of size 16:

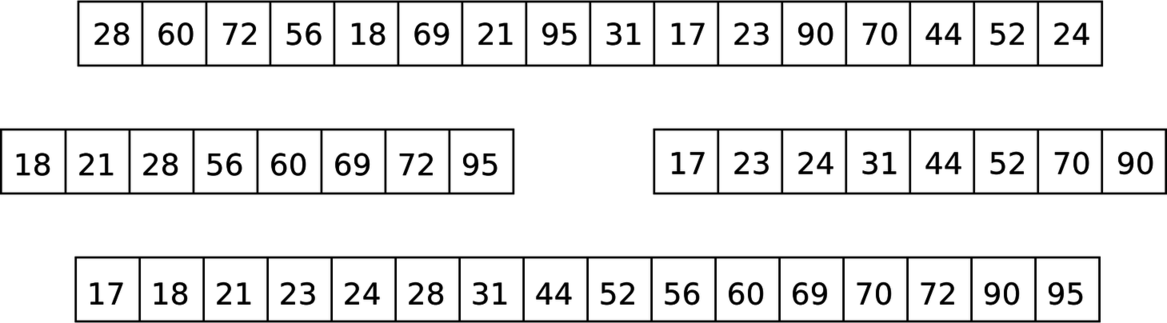
The line contains an unsorted array of 16 numbers. The second line shows the result after sorting the left and right halves of the array recursively. The third line shows the result of merging both of those sorted halves together again.

A Merge Sort Function

The following function implements this algorithm:


public static void mergeSort(int array[], int start, int end) {
    if(start < end) {
        // find the middle of the array
        int middle = (start + end) / 2;

        // sort the left half
        mergeSort(array, start, middle);

        // sort the right half
        mergeSort(array, middle + 1, end);

        // merge the two halves together
        merge(array, start, end);
    }   
}

This calls a function called "merge" which combines the two sorted halves together.

The Merge Function

The merge algorithm is given below:

Create a temporary array of the same size as the one to be merged.
Keep track of the indices in the left and right halves.
While both halves still have values:
1. Compare the next value in each half, and copy the smallest of the two to the next location in the temporary array.
Copy any remaining elements from the left half to the temporary array.
Copy any remaining elements from the right half to the temporary array.
Copy the temporary array back over the original one.

Below is a complete program which illustrates merge and merge sort:


import java.util.*;

public class MC { 
    public static final int SIZE = 25;

    // merge sort an array from a starting point to an ending point
    public static void mergeSort(int array[], int start, int end) {
        if(start < end) {
            // find the middle of the array
            int middle = (start + end) / 2;

            // sort left half
            mergeSort(array, start, middle);

            // sort right half
            mergeSort(array, middle + 1, end);

            // merge the two halves together
            merge(array, start, end);
        }
    }

    // merge an array which has its left and right halves sorted
    public static void merge(int array[], int start, int end) {
        // find the middle
        int middle = (start + end) / 2;

        // create a temporary array of the correct size
        int temp [] = new int[end - start + 1];
        int temp_index = 0;

        // keep track of indices for both halves
        int left = start;
        int right = middle + 1;

        // while both halves have data
        while((left <= middle) && (right <= end)) {
            // if the left half value is less than right
            if (array[left] < array[right]) {
                // take from left
                temp[temp_index] = array[left];
                temp_index++;
                left++;
            } else {
                // take from right
                temp[temp_index] = array[right];
                temp_index++;
                right++;
            }
        }

        // add the remaining elements from the left half
        while(left <= middle) {
            temp[temp_index] = array[left];
            temp_index++;
            left++;
        }

        // add the remaining elements from the right half
        while(right <= end) {
            temp[temp_index] = array[right];
            temp_index++;
            right++;
        }

        // move from temp array to the original array
        for(int i = start; i <= end; i++) {
            array[i] = temp[i - start];
        }
    }

    public static void main(String args[]) {
        int nums[] = new int [SIZE];
        // put in random numbers
        Random generator = new Random();
        for(int i = 0; i < SIZE; i++) {
            nums[i] = generator.nextInt(100);
        }

        // print them
        System.out.print("Unsorted numbers: ");
        for(int i = 0; i < SIZE; i++) {
            System.out.print(nums[i] + " ");
        }

        // sort them
        mergeSort(nums, 0, SIZE - 1);

        // print them again
        System.out.print("\nSorted numbers: ");
        for(int i = 0; i < SIZE; i++) {
            System.out.print(nums[i] + " ");
        }
        System.out.print('\n');
    }
}

Visualizations of merge sort, in addition to bubble sort and some other sorting algorithms, can be seen here: https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html.

Merge Sort vs. Bubble Sort

Merge sort is a little more complicated than the bubble sort algorithm we saw earlier, but it is significantly more efficient. Computer scientists quantify the efficiency of algorithms by relating the number of steps of the algorithm to the input size.

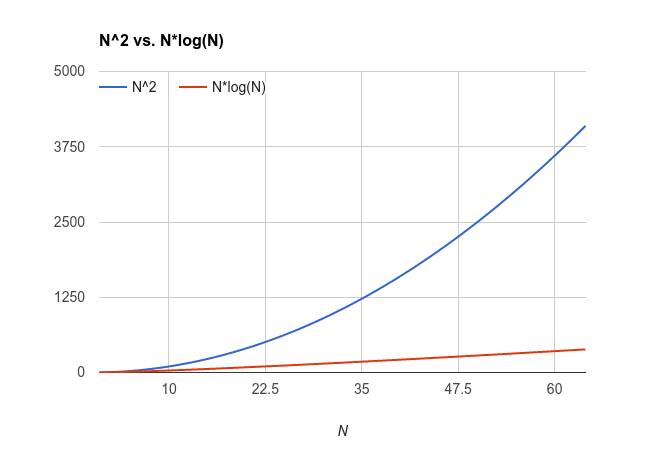
If the bubble sort algorithm is run on an array of size $N$, then it takes proportional to $N^2$ steps. The reasoning for this is because the "while not sorted" loop can run at most $N$ times, and the "for each item in the array" loop can also run $N$ times. Because they are nested the number of steps is $N^2$.

For merge sort but the number of steps is proportional to $N \times log_2(N)$. The reasoning for this is because the merge algorithm takes proportional to $N$ steps as it goes through the array one time. The algorithm is repeated as many times as we can divide the array in half until we hit the base case. The number of times you can divide $N$ in half before hitting 0 is $log_2(N)$.

Below is a graph of $N$ vs. $N \times log_2(N)$: