
Another graph problem is the travelling salesman problem. In this problem, there is a salesman who would like to visit all of a set of cities in order to sell their products. To do this, they need to make a tour of the cities where they visit each city exactly once and end up back where they started.
It is not possible to complete a tour for every graph. For example in the graph of Virginia cities given above it is not possible to complete a full tour and end up back where we started. For the graph below, however it is possible:
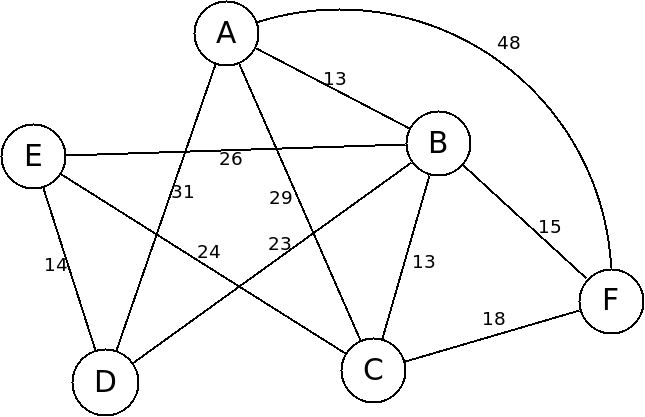
One tour is C-F-A-B-D-E-C. Another is from A-B-F-C-E-D-A. However these tours will take different amounts of time to complete based off of the edges we must take on the tour. The first will take 148 and the second will take 115. Clearly the salesman will prefer to take the second tour as it will cost him less time, gas or airfare.
The travelling salesman problem is to find the tour with the least total cost.
The number of possible tours through the graph is the same as the number of permutations of the cities in the graph. A permutation is a specific order of the cities. There are $N!$ permutations of $N$ cities.
The direct approach to solving the problem is to generate all $N!$ permutations, calculate the cost of each one, and see which is the longest. This is called a brute force approach and is illustrated in this example. This program goes through the possible permutations recursively.
The Big-O for this algorithm is actually the biggest we will see in this class! Because we try every permutation of $N$ nodes, this algorithm is actually $O(N!)$.
The graph below shows how complexities increase for $N$:
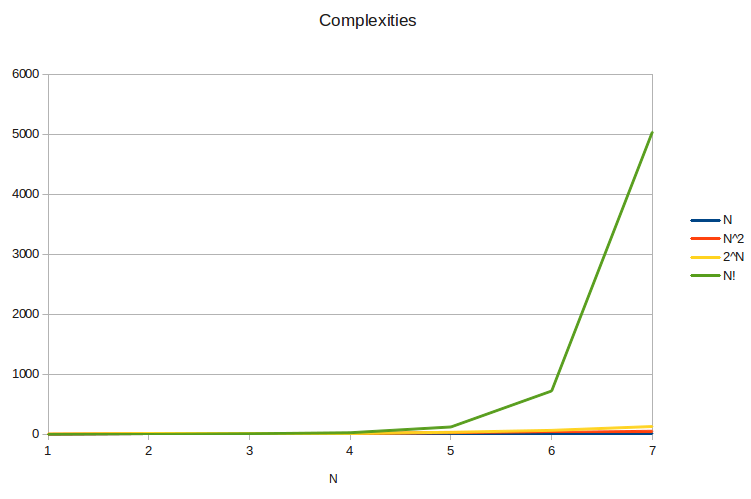
As you can see, $N!$ completely dwarfs even $2^N$ as $N$ increases.
In computer science, we classify problems in terms of how difficult they are to solve. Algorithms which have a Big-O complexity of the form $O(N^k)$ where $k$ is a constant are called polynomial problems. Even if an algorithm is $O(N^{1000})$ it is considered to be polynomial. Problems that have a polynomial algorithm are said to be in class $P$.
This means that the shortest path problem, the minimal spanning tree problem and most of the other problems we have looked at are in class $P$.
The travelling salesman problem has no known polynomial algorithm that can solve it. The best algorithm known is $O(N^2 \cdot 2^N)$. This problem belongs to a class of very hard programs called "$NP$-Complete" which have no polynomial time algorithms. Moreover, it's very unlikely that there even exists a polynomial algorithm to any $NP$-Complete problem. If you find one, you'll receive a $1,000,000 prize from the Clay Mathematics Institute.
Due to their open nature, graphs have several other $NP$-Complete problems associated with them:
These may sound esoteric, but many useful problems reduce to one of these difficult problems.
Scheduling problems can reduce to the graph coloring problem, as can the problem of allocating registers in a compiler.
The clique problem comes up in protein folding and gene modelling applications.
Being able to recognize these problems may keep you from spending time trying to solve an infeasible problem!
Copyright © 2025 Ian Finlayson | Licensed under a Creative Commons BY-NC-SA 4.0 License.